Movimento Circular Uniforme (MCU)

Conceitos do movimento circular uniforme

Neste tópico iremos abordar o estudo de partículas que estão sujeitas a determinada situação que a vincule a permanecer em um movimento com trajetória circular e com velocidade escalar sempre constante. Na natureza não é tão fácil de encontrar tais sistemas, mas existem situações onde podemos fazer uma aproximação e considerar que tal movimento acontece para que possamos extrair informações importantes do sistema.

Um exemplo comum é o exemplo de um ponto na extremidade de uma roda de bicicleta ou pneu de um automóvel, é fato que tanto a roda da bicicleta como o pneu do automóvel não são exatamente circulares, mas podemos considerar que são com certa precisão. Outro exemplo mais surpreendente é o estudo do átomo de Bohr, onde consideramos que o movimento dos elétrons em torno do núcleo é circular e com velocidade constante. É claro que isto não é bem verdade, mas quando fazemos considerações como estas nós simplificamos muito os cálculos e podemos extrair excelentes informações sobre o sistema. Antes de iniciar nosso estudo, vamos definir duas quantidades que serão úteis mais a frente.

Frequência (f): É uma quantidade física que é dada pela razão entre o número de vezes em que um evento se repete durante um intervalo tempo ∆t e o intervalo tempo ∆t, matematicamente


A frequência é dada em segundo -1 = s-1 ou equivalentemente em hertz (Hz).

Período (T): Dado um fenômeno que se repete com certa frequência, o período é uma quantidade física definida como sendo o tempo mínimo para que um ciclo seja realizado.

Podemos relacionar o período com a frequência, para isso basta considerarmos que n=1 e que ∆t=T na equação acima e com isso temos

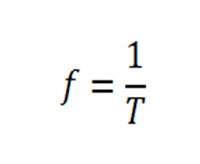
Assim vemos que a frequência é o inverso do período, pois fT=1.

Trajetória e espaço percorrido

Em cinemática nós sabemos que todo o estudo é feito sem qualquer menção aos agentes que causam o movimento do objeto a ser estudado, então aqui não será diferente.

Considere uma partícula em uma trajetória circular de raio R, então considerado que a mesma inicia seu movimento em um ponto O e termina em um ponto P, como mostra a figura abaixo.

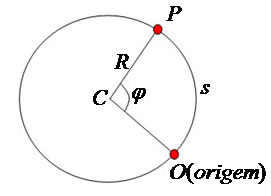
Então nós temos duas quantidades envolvidas que podem nos auxiliar no nosso estudo. A variação da posição angular φ (que chamaremos de distância angular percorrida) e a variação da posição escalar s (que chamaremos de distância linear percorrida). Se lembrarmos de bem de geometria de circunferências, saberemos que existe uma relação entre o ângulo φ (dado em radianos e denotado por rad) e o arco de circunferência, que no nosso caso é a distância percorrida s (que será dada em metros m). Tal relação é

onde R também deve ser dado em metros. Devemos sempre ter cuidado em movimento circular com as quantidades distância percorrida e deslocamento. Devemos sempre lembrar que deslocamento está diretamente relacionada com a posição do objeto, então se no instante inicial a posição é a mesma da posição ao final do movimento, então temos deslocamento nulo, mas isso não quer dizer que a distância percorrida também será, pois a distância percorrida é definida como a soma, em módulo, de todos os deslocamentos. Se tratando do termo deslocamento, nós temos duas opções. Em movimentos circulares nós podemos descartamos a existência do termo deslocamento devido ao fato de que existem duas quantidades definidas como Frequência e Período que nos induz a não existência de deslocamentos nulos. Ou simplesmente considerar a o termo deslocamento e apenas analisarmos sempre o movimento circular impondo que 0 < = ϕ < 2π pois quando ϕ = 0 e ϕ = 2π, nós teremos sempre a partícula na mesma posição. Então aqui nós não vamos mais voltar a mencionar o termo deslocamento para que ϕ possa ser qualquer número real.

A velocidade angular escalar média.

Sabemos que no movimento retilíneo e uniforme (MRU) nós definimos uma quantidade que nos diz o quão rápido um objeto se distância de sua posição inicial, que chamamos de velocidade linear escalar média. Então como podemos definir a mesma quantidade para o movimento circular? Existe uma quantidade que nos diz o quão rápido um objeto se distancia de sua posição inicial? A resposta claramente é sim. Em qualquer movimento sempre existirá uma velocidade escalar, logo podemos defini-la em movimentos circulares. Definimos aqui a velocidade escalar média v como sendo a razão entre a distância linear percorrida e o intervalo de tempo para que o objeto percorra essa distância, matematicamente temos que

Nós também podemos definir uma quantidade conhecida como velocidade angular média, nós agora vamos mostrar como determinar essa quantidade. Considere a equação (4) como uma forma padrão de calcularmos a velocidade, e substituiremos o valor de s da equação (3), com isso ficamos com

Como o movimento tem velocidade v constante, vamos analisar o caso de uma única volta, e com isso temos que o intervalo tempo do movimento é exatamente igual ao período (devido a forma como definimos o período. Então para uma volta completa temos ϕ = 2π e ∆t = T, resultando em

Esta é a expressão para a velocidade linear escalar. Note que a quantidade 2π/T como se fosse uma velocidade com dimensão de rad/s, devido a essa analogia, nós definimos a velocidade angular escalar como sendo

A última igualdade é verdade por causa da equação (2). Por fim, desde que conheçamos a velocidade angular, podemos determinar a velocidade linear pela equação

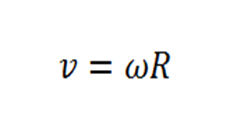
Com essas equações nós podemos estudar e caracterizar completamente o movimento de qualquer partícula que esteja em movimento circular e uniforme. É importante lembrar que todas as equações envolvendo as velocidades angular e linear são equivalentes, assim o uso de uma ou outra equação depende apenas dos dados fornecidos pela questão. Por exemplo, se na questão nos é fornecido o valor da velocidade angular ω e o raio R, então é conveniente usarmos diretamente a equação (8) para determinar a velocidade linear v. Se nos é fornecido o período T e o raio R, podemos proceder de duas formas: 1) usar a equação (7) para determinar a velocidade angular ω e depois usar a equação (8) para determinar a velocidade linear v, ou 2) podemos usar diretamente a equação (6) para este fim.

Texto enviado pelo professor de física Alan Costa dos Santos.

Veja aqui mais tirinhas de Física.