Lançamento Oblíquo

Estudaremos neste texto o lançamento oblíquo. Um lançamento oblíquo, ou movimento oblíquo, é o movimento com um ângulo acima da horizontal, onde consideramos duas dimensões, x e y. Na tirinha vestibulário “Professor, o técnico” temos um exemplo de lançamento oblíquo, vamos analisar este exemplo:

Tirinha de física sobre lançamento oblíquo

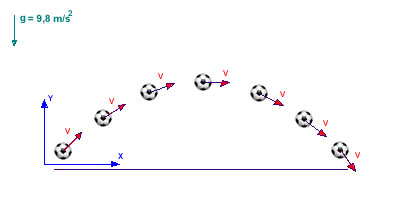
A imagem abaixo mostra o lançamento de uma bola de futebol que perfaz uma trajetória parabólica.

Observe na imagem que para cada ponto existe um vetor velocidade diferente do anterior. Para estudar este tipo de movimento, vamos dividi-lo em dois. Um movimento na horizontal e outro na vertical, isto porque a aceleração gravitacional é a única a modificar o vetor velocidade.

Observe a próxima figura:

Nesta imagem vemos os dois movimentos que compostos formam o lançamento oblíquo. Na direção horizontal não existe nenhuma aceleração, logo, a componente horizontal da velocidade (Vx) é sempre uma constante, ou seja, este movimento é uniforme.

Na direção vertical a aceleração da gravidade age sobre o objeto, sendo que a componente vertical da velocidade (Vy) é máxima no ponto mais baixo e, zero no ponto mais alto quando o objeto para e inicia sua queda. Este movimento é, então, um movimento uniformemente variado.

Dividindo o lançamento oblíquo em dois movimentos já conhecidos, podemos analisá-lo com as equações já estudadas anteriormente nos textos movimento uniforme e movimento uniformemente variado. Para isto, devemos decompor a velocidade nas direções x e y utilizando as relações de um triangulo retângulo.

Se um objeto é lançado com velocidade V em um ângulo θ com a horizontal, analisamos os vetores velocidade para formar um triângulo retângulo da seguinte maneira:

Observando o triângulo vemos que:

senθ = Vy / V

cosθ = Vx / V

Logo:

Vy = senθ . V 

Vx = cosθ . V

Também vale a relação de Pitágoras:

V2=Vx2 + Vy2

Bem, já sabemos como decompor a velocidade e analisar o lançamento oblíquo em duas direções, agora vamos resolver um exercício.

Exercício resolvido sobre lançamento oblíquo

(Cefet-CE) Um aluno do Cefet em uma partida de futebol lança uma bola para cima, numa direção que forma um ângulo de 60o com a horizontal. Sabendo que a velocidade na altura máxima é 20 m/s, podemos afirmar que a velocidade de lançamento da bola, em m/s, será:

a) 10

b) 17

c) 20

d) 30

e) 40

Vimos que no ponto mais alto da trajetória a velocidade na vertical (Vy) é nula, ou seja, o objeto tem apenas velocidade na horizontal (Vx) que neste caso vale, então, 20 m/s. Sendo assim:

Vx = cosθ . V

20 = cos 60o . V

20 = ½ . V

Ou seja,

½ . V = 20

V = 20 . 2/1

V = 40m/s

Obtemos como resposta a alternativa e.

Exercício do ENEM sobre lançamento oblíquo

(Enem PPL 2014) Na Antiguidade, algumas pessoas acreditavam que, no lançamento oblíquo de um objeto, a resultante das forças que atuavam sobre ele tinha o mesmo sentido da velocidade em todos os instantes do movimento. Isso não está de acordo com as interpretações científicas atualmente utilizadas para explicar esse fenômeno.

Desprezando a resistência do ar, qual é a direção e o sentido do vetor força resultante que atua sobre o objeto no ponto mais alto da trajetória?

a) Indefinido, pois ele é nulo, assim como a velocidade vertical nesse ponto.
b) Vertical para baixo, pois somente o peso está presente durante o movimento.
c) Horizontal no sentido do movimento, pois devido à inércia o objeto mantém seu movimento.
d) Inclinado na direção do lançamento, pois a força inicial que atua sobre o objeto é constante.
e) Inclinado para baixo e no sentido do movimento, pois aponta para o ponto onde o objeto cairá.

Um bom exemplo de lançamento oblíquo é o de uma bola lançada por um canhão.

Desprezando a resistência do ar, a única força que age no corpo em movimento oblíquo após o seu lançamento é a força peso. Pensando no exemplo, o canhão exerceu uma força no momento em que a bola de ferro é lançada, e esta descreve uma trajetória parabólica, mas após perder o contato com o canhão resta apenas a gravidade agindo nesse corpo, o que resulta em uma força peso. Esta força tem direção vertical e sentido para baixo.

A resposta é a letra b.

Espero que o texto tenha ajudado a tirar suas dúvidas sobre o lançamento oblíquo.