O eletromagnetismo e as equações de Maxwell

Neste texto veremos uma pouco mais sobre a evolução do eletromagnetismo, conheceremos as descobertas de Maxwell e as brilhantes equações de Maxwell.

James Clerk Maxwell (1831 – 1879) se propôs a elaborar uma teoria matemática para as descobertas de Faraday e, assim, conseguiu unificar matematicamente a eletricidade, o magnetismo e a óptica, mostrando que a luz é uma vibração do campo eletromagnético se propagando no espaço.

Esta descoberta foi apresentada por Maxwell através de, mais ou menos, vinte equações que depois foram sintetizadas, por outros matemáticos, e apresentadas na forma de quatro equações que conhecemos hoje como equações de Maxwell.

Abaixo temos as equações de Maxwell, mas é importante lembrar que esta forma é valida para o vácuo.

Onde:
é a densidade de carga
E é o campo elétrico

A partir desta primeira equação podemos dizer que as linhas de campo elétrico saem das cargas elétricas positivas e entram nas cargas negativas.

Onde:

c é a velocidade da luz no vácuo
B é o campo magnético

Esta equação nos diz que um campo magnético variável induz um campo elétrico.

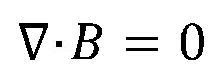
Onde:

B é o campo magnético

A partir desta equação podemos dizer que o campo magnético sempre constitui uma linha fechada, ou seja, nunca converge ou diverge.

Onde:

J é a densidade de corrente
B é o campo magnético
E é o campo elétrico

De onde podemos dizer que linhas de campo magnético circulam em torno de campos elétricos variáveis.